Les maths, c'est carré
-
@Peri en fait ça se base sur la décomposition des nombres en unité, dizaine, centaines etc, c est juste enrobé de 2 ou 3 operations qui sont la pour t embrouiller et qui s annulent mutuellement. Regarde ce que ça donne une fois écrit
Si tu prends le nombre a 7 chiffres que tu decoupes en
x les 3 premiers chiffres
y les 4 derniers chiffresRentrez les 3 premiers chiffres de votre nombre
Multipliez par 80-> 80 x
Ajoutez 1
-> 80 x + 1
Multipliez par 250
-> 20000 x + 250
Ajoutez le nombre constitué des 4 derniers chiffres de votre nombre
-> 20000 x + 250 + y
Recommencez l'étape précédente
-> 20000 x + 250 + 2 y
Soustrayez 250
-> 20000 x + 2 y
Divisez par 2
au final tu obtiens
-> 10000 x+ yet justement 10000 x ça decale x de 4 chiffres vers la gauche donc ça redevient les 3 premiers chiffres d un nombre a 7 chiffres. Tu ajoutes y qui sont les 4 chiffres de fin et tu retrouves ton nombre de départ
Si tu prends le nombre a 7 chiffres 1234567
x les 3 premiers chiffres: x = 123
y les 4 derniers chiffres: y = 4567
10000 x + y = 10000 * 123 + 4567 = 1234567 -
Un démonstration limpide mon cher @icescream . Une fois la mécanique décortiquée, c'est parfaitement logique en effet. Merci.

-
Les gens à l'esprit mathématiques comme ça, ça me dépasse totalement ! Waouw

Mais effectivement, c'est hyper limpide, même moi, j'ai compris !
! -
-
@Fenixia tu me rassures, je me sens moins seule.

-
-
SOS. Pitié.
Ca va faire 2h30 que j'insulte mon voisin, que j'envoie paître Egon jusqu'à Rouen, tout ça parce que je bite rien à un exercice de con avec un x et un y de je sais pas quoi.J'essaie de me remettre à la page sur 2 ou 3 trucs scolaires, histoire de ne pas insulter l'avenir si je me résous à changer de voie de boulot un jour. Comprendre avant que mon dos ne casse.
Je démonte des raies dés qu'il faut écrire ou envoyer la sauce à partir d'un texte mais pour les chiffres, mon camarade, je stresse.
Voici le grave problème :
Y a 4 parkings dans la ville. Parking A , B , C et D.
Le A est à 100m du centre ville
Le B à 400m
Le C à 850m
Le D à 1300mL'ensemble de ces parkings doivent donner un coût total de 6 euros. Plus t'es proche du centre ville, plus tu payes cher et plus tu t'éloignes, plus tu as de l'argent pour payer le subway à madame.
Donc le tarif du parking A 4,15e
Le B 1,04e
Le C 0,49e
Le D 0,32eJ'ai craqué psychologiquement donc après 2h de combat, j'ai donc le résultat final mais je suis foutrement incapable de trouver la formule niveau CP qui donne ses chiffres de 4,15 pour le A etc etc.
Je m'enfile des cours youtube de coefficient (de mon cul j'insiste) K proportionnel inverse, de X, de Y en veux tu en voilà mais avec pour seul résultat de me faire péter ma dernière chandelle d'espoir.
Je suis chaud pour attaquer derrière la cosmologie et remettre en cause les équations d'Einstein mais si avant ça quelqu'un, que dis-je un Dieu des maths pouvait me donner l'astuce et la formule pour arriver aux résultats que j'ai énoncé au niveau des tarifs, je lui vouerai un culte jusqu'à minimum ce soir 23h59.
-
-
@jool Merci pour ton effort...
Malheureusement, et ça c'est pas de ta faute, tu as en ta compagnie la tête de bite la plus célèbre de la Nouvelle-Aquitaine et ça c'est pas rien.
Ce chiffre de 415 il vient d'ou cet enfoiré?
Je rajoute que j'ai également en ma possession un coefficient K proportionnel inverse de 0,16 et lui non plus je sais pas ce qu'il vient foutre là.
Je divise 1 par 400 que je multiplie etc etc mais le 415 il est nul part.
Je bouillonne d'être aussi con. -
@Koursk
Le détail :
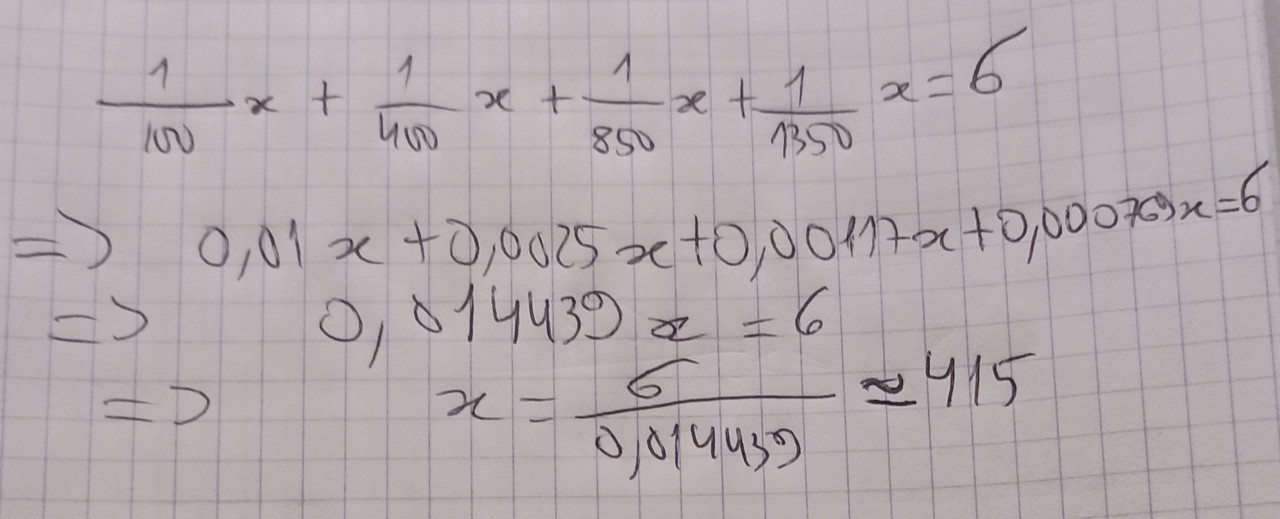
Pour bien faire j'aurais dû mettre x en facteur, puis réduire au même dénominateur les fractions pour donner un calcul plus "beau". Là j'ai juste remplacé les 1/100 par 0.01 etc...
-
Trop fort @jool
Je m'arrache les cheveux depuis tout à l'heure. En tout cas, c'est pas du CP ! -
Arf Jool a repondu avant moi

j'etais sur le meme chemin juste que la mise en denominateur commun est un poil casse pied a faire
ce qui donne
x=6*(176800/2554) -
@jool C'est hyper chaud ce bordel. Non non, y a rien à comprendre. La phrase que tu as écrite avec ta capture d'écran, c'est simple, je ne comprends pas un traître mot et cela me rappelle pourquoi on m'a mis un stop pour la seconde générale.
J'ai suivi pas à pas ton calcul et je merde au niveau de la division de 1 par 1350. J'ai 0,0007407. Mon résultat varie et du coup je retrouve à chaque coup 418. Du coup, mes chiffres à la fin sont différents pour la répartition.
Bref, j'ai en tout cas sur le papier, une méthodologie qui me permettra sans doute d'avancer et un beau jour j'aurai les mêmes chiffres. Notamment ce 415 des enfers. Egon te remercie également car cela évitera une séparation vu l'état dans lequel je suis.
Merci babe.
Edit 1 Putain c'est bon. J'ai rien dit
Edit 2 j'avais fait n'importe quoi
Edit 3 le show continue merci -
-
@Koursk
Oups pardon c'est 1300 et pas 1350, heureusement j'avais fait le calcul avant avec les bonnes distances
-
@jool J'ai décidé de te pardonner.



